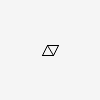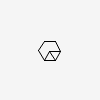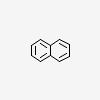Compute the shortest cycles through each vertex triple. This allows one to
directly obtain the envelope rings of bicyclic fused system. These cycles
can be thought of as the 'ESSSR' (extended smallest set of smallest rings)
and 'envelope' rings as used by PubChem fingerprints (CACTVS Substructure
Keys). The PubChem fingerprint documentation exclusively refers to the ESSSR
and envelopes as just the ESSSR and the rest of this documentation does the
same. This class provides the cycles (vertex paths) for each ring in the
ESSSR.
The ESSSR should not be confused with the extended set of smallest rings
(ESSR) [Downs, G and Gillet, V and Holliday, J, and Lynch, M,
Theoretical Aspects of Ring Perception and Development of the Extended Set of Smallest Ring Concepts, J. Chem. Inf. Comput. Sci,
1989, 29:187-206].
Algorithm To our knowledge no algorithm has been published for
the ESSSR. The
PubChem
Specifications states -
"An ESSSR ring is any ring which does not
share three consecutive atoms with any other ring in the chemical structure.
For example, naphthalene has three ESSSR rings (two phenyl fragments and the
10-membered envelope), while biphenyl will yield a count of only two ESSSR
rings". The name implies the use of the smallest set of smallest rings
(SSSR). Not every graph has an SSSR and so the minimum cycle basis is used
instead. With this modification the algorithm is outlined below.
- Compute a minimum cycle basis (or SSSR) of the graph (may not be
unique)
- For each vertex v and two adjacent vertices (u
and w) check if the path -u-v-w- belongs to any cycles already
in the basis
- If no such cycle can be found compute the shortest
cycle which travels through -u-v-w- and add it to the basis. The
shortest cycle is the shortest path from u to w which does not
travel through v
In the case of
naphthalene the
minimum cycle basis is the two phenyl rings. Taking either bridgehead atom of
naphthalene to be
v and choosing
u and
w to be in
different phenyl rings it is easy to see the shortest cycle through
-u-v-w- is the 10 member envelope ring.
Canonical and Non-Canonical Generation
The algorithm can generate a canonical or non-canonical (preferred) set of
cycles. As one can see from the above description depending on the order we
check each triple (-u-v-w-) and add it to basis we may end up with a
different set.
To avoid this PubChem fingerprints uses a canonical labelling ensuring the
vertices are always checked in the same order. The vertex order used by this
class is the natural order of the vertices as provided in the graph. To
ensure the generated set is always the same vertices should be ordered
beforehand or the non-canonical option should be used.
Although this canonical sorting allows one to reliable generate the same set
of cycles for a graph this is not true for subgraphs. For two graphs
G,
H and a canonical ordering (
π). If
H is a
subgraph of
G then for two vertices
u,
v. It follows
that
π(u) <
π(v) ∈
H ⇏
π(u) <
π(v) ∈
G. In other words, we can canonically label a graph and inspect the
ordering of vertices
u and
v. We now take a subgraph which
contains both
u and
v - the ordering does not need to be the
same as the full graph. This means that a subgraph may contain a ring in its
ESSSR which does not belong to the ESSSR of the full graph.
To resolve this problem you can turn off the
canonical option. This
relaxes the existing condition (Step 2.) and adds all shortest cycles through
each triple (-u-v-w-) to the basis. The number of cycles generated may be
larger however it is now possible to ensure that if
H is a subgraph of
G then ESSSR of
H will be a subset of the ESSSR or
G.
Alternatively one may consider using the
RelevantCycles which is the
the smallest set of short cycles which is
uniquely defined for a
graph.
To better explain the issue with the canonical labelling several examples are
shown below. The table outlining the size of rings found for each molecule
when using canonical and non-canonical generation. Also shown are the sizes
of rings stored in the PubChem fingerprint associated with the entry. The
fingerprints were obtained directly from PubChem and decoded using the
specification. Sizes underlined and coloured red represent rings which may
or may not be present depending on the atom ordering. It can be seen from the
PubChem fingerprint that even using a consistent canonical labelling rings
may be absent which would be present if the subgraph was used.
| PubChem CID | Diagram | Size of Rings in
ESSSR
(fingerprints only store cycles |C| <=
10) | Source |
|---|
|
| CID 135973 |
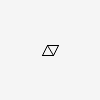 |
| {3, 3, 4} |
| {3, 3, 4} |
| {3, 3, 4} |
|
| Canonical |
| Non-canonical |
| PubChem Fingerprint |
|
| CID 9249 |
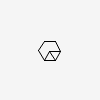 |
| {3, 3, 4, 6, 6} |
| {3, 3, 4, 6, 6} |
| {3, 3, 6, 6} |
|
| Canonical - 4 member cycle only added if found before larger 6
member cycles |
| Non-canonical |
| PubChem Fingerprint - 4 member cycle not found |
|
| CID 931 |
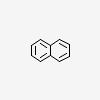 |
| {6, 6, 10} |
| {6, 6, 10} |
| {6, 6, 10} |
|
| Canonical |
| Non-canonical |
| PubChem Fingerprint |
|
| CID 5702 |
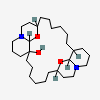 |
| {6, 6, 6, 6, 10, 10, 20, 22, 22, 24, 24} |
| {6, 6, 6, 6, 10, 10, 20, 22, 22, 24, 24} |
| {6, 6, 6, 6} |
|
| Canonical - 10 member cycles only added if found before larger
cycles |
| Non-canonical |
| PubChem Fingerprint - 10 member cycles not found |
|
| CID 1211 |
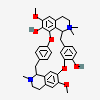 |
| {6, 6, 6, 6, 6, 6, 10, 10, 18, 18, 20, 20, 22, 22, 22} |
| {6, 6, 6, 6, 6, 6, 10, 10, 18, 18, 20, 20, 22, 22, 22} |
| {6, 6, 6, 6, 6, 6, 10, 10} |
|
| Canonical - 10 member cycles only added if found before larger
cycles |
| Non-canonical |
| PubChem Fingerprint - 10 member cycles were found |
|
| CID 17858819 |
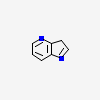 |
| {5, 6, 9} |
| {5, 6, 9} |
| {5, 6, 9} |
|
| Canonical |
| Non-canonical |
| PubChem Fingerprint |
|
| CID 1909 |
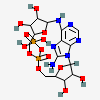 |
| {5, 5, 5, 6, 9, 16, 17, 17,
17,
18} |
| {5, 5, 5, 6, 9, 16, 17, 17, 17, 18} |
| {5, 5, 5, 6} |
|
| Canonical - 9 member cycle only added if found before larger
cycles |
| Non-canonical |
| PubChem Fingerprint - 9 member cycle not found |
|